ΚΛΑΣΜΑΤΑ - ΓΕΝΙΚΑ ΣΤΟΙΧΕΙΑ
Γενικά στοιχεία για τα κλάσματα
ΣΥΓΚΡΙΣΗ ΚΛΑΣΜΑΤΩΝ
Πώς συγκρίνουμε ομώνυμα κλάσματα
Όταν δύο κλάσματα είναι ομώνυμα, μεγαλύτερο είναι εκείνο που έχει τον μεγαλύτερο αριθμητή.
Παραδείγματα
  |  |
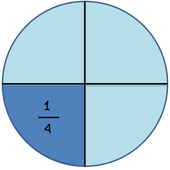
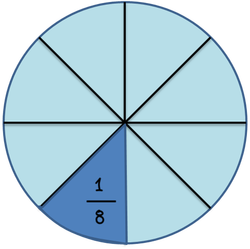
Πώς συγκρίνουμε ετερώνυμα κλάσματα
Μεγαλύτερο είναι εκείνο που έχει το μικρότερο παρονομαστή.
Παράδειγμα
 |  |  |  |
Α΄ τρόπος
Μετατρέπουμε τα ετερώνυμα κλάσματα σε δεκαδικούς αριθμούς και τα συγκρίνουμε.
Παράδειγμα
|  |
Β΄ τρόπος
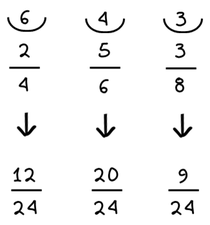
Μετατρέπουμε τα ετερώνυμα κλάσματα σε ομώνυμα και τα συγκρίνουμε.
ΜΕΓΑΛΩΝΩ & ΜΙΚΡΑΙΝΩ ΕΝΑ ΚΛΑΣΜΑ
Για να μεγαλώσω ένα κλάσμα...
ή
Παράδειγμα
Για να μικρύνω ένα κλάσμα...
ή
Παράδειγμα
Β΄ τρόπος
Μετατρέπουμε τα ετερώνυμα κλάσματα σε ομώνυμα και τα συγκρίνουμε.
ΜΕΤΑΤΡΟΠΗ ΚΛΑΣΜΑΤΟΣ ΣΕ ΔΕΚΑΔΙΚΟ ΑΡΙΘΜΟ
& ΤΟ ΑΝΤΙΣΤΡΟΦΟ
Για να μετατρέψουμε ένα κλάσμα σε δεκαδικό αριθμό, διαιρούμε τον αριθμητή με τον παρονομαστή.
Παράδειγμα
Τον αριθμό αυτόν μπορούμε να τον γράψουμε και ως δεκαδικό κλάσμα
|  |
Αν μια διαίρεση δε δίνει ακριβές πηλίκο, τότε υπολογίζουμε το πηλίκο κατά προσέγγιση (περίπου) και σταματάμε στα χιλιοστά.
Παράδειγμα
ΜΕΤΑΤΡΟΠΗ ΚΛΑΣΜΑΤΟΣ ΣΕ ΜΕΙΚΤΟ ΑΡΙΘΜΟ
& ΤΟ ΑΝΤΙΣΤΡΟΦΟ
 |  |  |
Για να μετατρέψουμε γρήγορα ένα κλάσμα (καταχρηστικό) σε μεικτό αριθμό...
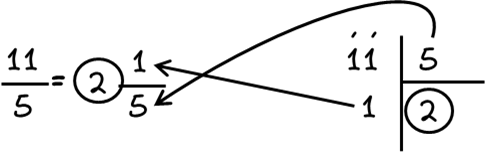
1. Διαιρούμε τον αριθμητή με τον παρονομαστή.
2. Το πηλίκο της διαίρεσης είναι ο ακέραιος του μεικτού.
3. Το κλάσμα του μεικτού έχει αριθμητή το υπόλοιπο της διαίρεσης και παρονομαστή τον ίδιο με το αρχικό κλάσμα.
2. Το πηλίκο της διαίρεσης είναι ο ακέραιος του μεικτού.
3. Το κλάσμα του μεικτού έχει αριθμητή το υπόλοιπο της διαίρεσης και παρονομαστή τον ίδιο με το αρχικό κλάσμα.
Παράδειγμα
Αν διαιρέσουμε τους όρους ενός καταχρηστικού κλάσματος, θα μας προκύψει ή ακέραιος ή μεικτός αριθμός.
|  |
|
Για να μετατρέψουμε γρήγορα ένα μεικτό αριθμό σε κλάσμα...
1. Πολλαπλασιάζουμε τον ακέραιο του μεικτού με τον παρονομαστή του κλάσματός του.
2. Στο γινόμενο που προκύπτει προσθέτουμε τον αριθμητή του μεικτού αριθμού.
3. Το αποτέλεσμα αποτελεί τον αριθμητή του νέου κλάσματος, ενώ παρονομαστής παραμένει ο ίδιος.
2. Στο γινόμενο που προκύπτει προσθέτουμε τον αριθμητή του μεικτού αριθμού.
3. Το αποτέλεσμα αποτελεί τον αριθμητή του νέου κλάσματος, ενώ παρονομαστής παραμένει ο ίδιος.
Παράδειγμα
 |  |
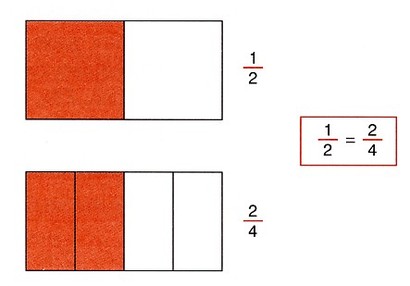
ΙΣΟΔΥΝΑΜΑ ΚΛΑΣΜΑΤΑ
Δύο ή περισσότερα κλάσματα που έχουν διαφορετικούς όρους, δηλαδή διαφορετικό αριθμητή & παρονομαστή, αλλά εκφράζουν την ίδια ποσότητα, λέγονται ισοδύναμα.
Π.χ.  |
Για να βρούμε αν δύο κλάσματα είναι ισοδύναμα, πολλαπλασιάζουμε τους όρους σταυρωτά (σταυρωτά ή χιαστί γινόμενα).
Αν τα σταυρωτά γινόμενα είναι ίσα, τότε είναι ισοδύναμα. Αν τα σταυρωτά γινόμενα είναι άνισα, τότε δεν είναι ισοδύναμα. |  |
Δημιουργώ ισοδύναμα κλάσματα πολλαπλασιάζοντας ή διαιρώντας και τους δύο όρους ενός κλάσματος με τον ίδιο αριθμό.
Όταν πολλαπλασιάζω και τους δύο όρους του κλάσματος, δημιουργώ ένα ισοδύναμο κλάσμα με μεγαλύτερους όρους.
| 
Όταν διαιρώ και τους δύο όρους του κλάσματος με τον ίδιο αριθμό, δημιουργώ ένα ισοδύναμο κλάσμα με μικρότερους όρους.
Η διαδικασία αυτή ονομάζεται απλοποίηση (το κλάσμα γίνεται πιο απλό). |
 |
Όταν ένα κλάσμα δεν μπορεί να απλοποιηθεί, δεν υπάρχει δηλαδή αριθμός που να διαιρεί ακριβώς και τον αριθμητή και τον παρονομαστή, τότε το κλάσμα λέγεται ανάγωγο.
Για να απλοποιήσω ένα κλάσμα και να το κάνω ανάγωγο, χρησιμοποιώ το Μ.Κ.Δ. με τον οποίο διαιρώ και τους δύο όρους του κλάσματος.
ΜΕΤΑΤΡΟΠΗ ΕΤΕΡΩΝΥΜΩΝ ΚΛΑΣΜΑΤΩΝ
|
 |
ΕΛΑΧΙΣΤΟ ΚΟΙΝΟ ΠΟΛΛΑΠΛΑΣΙΟ (Ε.Κ.Π)
ΠΡΟΣΘΕΣΗ & ΑΦΑΙΡΕΣΗ ΚΛΑΣΜΑΤΩΝ
ΠΡΟΣΘΕΣΗ & ΑΦΑΙΡΕΣΗ ΟΜΩΝΥΜΩΝ ΚΛΑΣΜΑΤΩΝ
Πρόσθεση ομώνυμων κλασμάτων
 |
Προσθέτουμε τους αριθμητές και αφήνουμε τον ίδιο παρονομαστή.
|
Αφαίρεση ομώνυμων κλασμάτων
 |
Αφαιρούμε τους αριθμητές και αφήνουμε τον ίδιο παρονομαστή.
|
Πρόσθεση μεικτών αριθμών
Μετατρέπουμε τους μεικτούς σε κλάσματα
και προσθέτουμε.  |
ή
 |
Προσθέτουμε χωριστά τους ακέραιους
και χωριστά τα κλάσματα.  |
Αφαίρεση μεικτών αριθμών
Μετατρέπουμε τους μεικτούς σε κλάσματα
και αφαιρούμε.  |
ή
 |
Αφαιρούμε χωριστά τους ακέραιους
και χωριστά τα κλάσματα.  |
ΠΡΟΣΘΕΣΗ & ΑΦΑΙΡΕΣΗ ΕΤΕΡΩΝΥΜΩΝ ΚΛΑΣΜΑΤΩΝ
 |
Για να προσθέσουμε ή να αφαιρέσουμε ετερώνυμα κλάσματα, πρέπει πρώτα να τα μετατρέψουμε σε ομώνυμα. Εδώ μπορείς να θυμηθείς πώς γίνεται η μετατροπή.
Παράδειγμα  |
Αν έχουμε μεικτούς αριθμούς που τα κλασματικά τους μέρη είναι ετερώνυμα κλάσματα, τους μετρατρέπουμε πρώτα σε κλάσματα και μετά μετατρέπουμε τα ετερώνυμα κλάσματα σε ομώνυμα.
ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ & ΔΙΑΙΡΕΣΗ ΚΛΑΣΜΑΤΩΝ
Πολλαπλασιασμός κλασμάτων
Για να πολλαπλασιάσουμε δύο κλάσματα, σχηματίζουμε ένα νέο κλάσμα που έχει στον αριθμητή το γινόμενο των αριθμητών και στον παρονομαστή το γινόμενο των παρονομαστών.
Παράδειγμα
Με όποια σειρά κι αν πολλαπλασιάσουμε δύο κλάσματα το αποτέλεσμα είναι το ίδιο.
Παράδειγμα
 |  |  |
Κάθε ακέραιος μπορεί να γραφτεί ως κλάσμα με παρονομαστή τη μονάδα.
Παράδειγμα
 |  |  |
Αντίστροφοι αριθμοί
Δύο αριθμοί λέγονται αντίστροφοι, όταν το γινόμενό τους είναι ακριβώς 1.
 |  |  |
 |
Πολλαπλασιασμός ακέραιου αριθμού με κλάσμα
|
Αν θέλουμε να πολλαπλασιάσουμε ακέραιο αριθμό με κλάσμα, πολλαπλασιάζουμε τον ακέραιο μόνο με τον αριθμητή του κλάσματος…
Παράδειγμα
ή κάνουμε τον ακέραιο κλάσμα (βάζοντας στον παρονομαστή τη μονάδα) και στη συνέχεια κάνουμε πολλαπλασιασμό κλασμάτων.
 |
Πολλαπλασιασμός μεικτού αριθμού με κλάσμα
|
Αν θέλουμε να πολλαπλασιάσουμε μεικτό αριθμό με κλάσμα, μπορούμε να μετατρέψουμε το μεικτό αριθμό σε κλάσμα και στη συνέχεια να κάνουμε πολλαπλασιασμό κλασμάτων.
Παράδειγμα
 |
Πολλαπλασιασμός δεκαδικού αριθμού με κλάσμα
|
Αν θέλουμε να πολλαπλασιάσουμε δεκαδικό αριθμό με κλάσμα, μπορούμε να μετατρέψουμε το δεκαδικό αριθμό σε δεκαδικό κλάσμα και στη συνέχεια να κάνουμε πολλαπλασιασμό κλασμάτων.
Παράδειγμα
Διαίρεση κλασμάτων
Για να διαιρέσουμε δύο κλάσματα, αντιστρέφουμε τους όρους του δεύτερου κλάσματος (δηλαδή τον αντίστροφο αριθμό του διαιρέτη) και κάνουμε πολλαπλασιασμό.
Παράδειγμα
|
Μερικές ακόμα πληροφορίες για τη διαίρεση κλασμάτων
 |
Ο πολλαπλασιασμός και η διαίρεση είναι πράξεις αντίστροφες.
Αν θέλω να διαιρέσω έναν αριθμό με το 2 για παράδειγμα μπορώ να το κάνω ως εξής:
Δηλαδή να διαιρέσω με το 2 ή να πολλαπλασιάσω με το 1/2 που είναι ο αντίστροφος του αριθμού 2.
|
Και κάτι ακόμα...
Μπορώ να κάνω διαίρεση κλασμάτων μετατρέποντας τα κλάσματα σε ομώνυμα και βρίσκοντας πόσες φορές χωράει το ένα στο άλλο.
Παράδειγμα
Παράδειγμα
 |  |
 |  |
 |  |
χωράει 2 φορές στο
|  |
 |  |
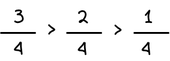
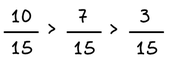
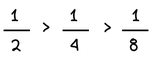
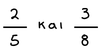
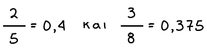
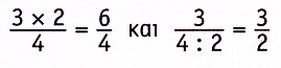
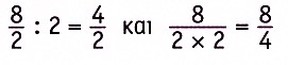
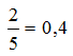
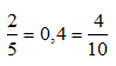
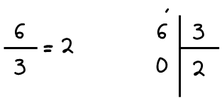
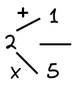
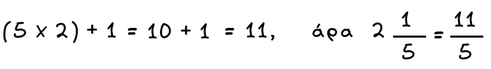
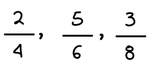
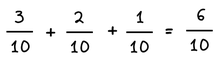
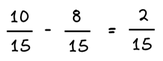
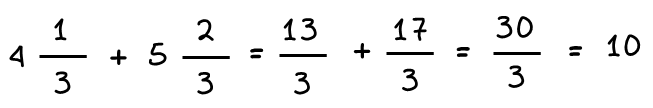
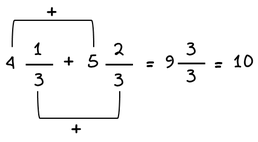
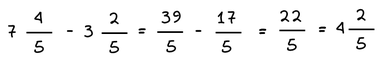
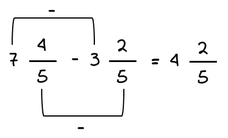
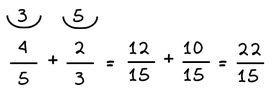
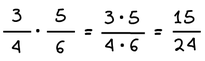
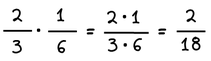
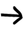
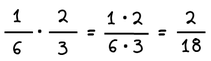
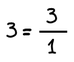
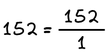
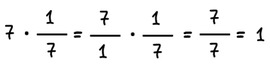
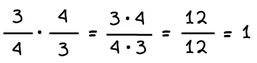
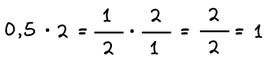
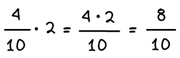
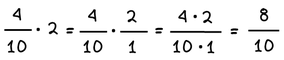
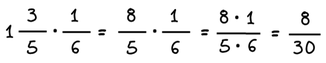
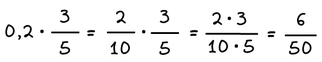
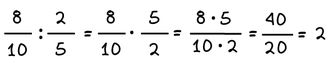
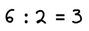
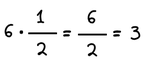
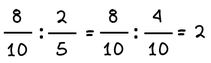
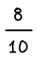
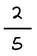
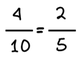
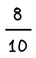
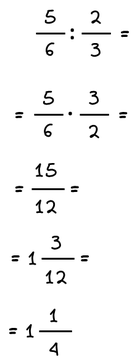
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου